1. Một số khái niệm cơ bản:
- Quần thể: toàn bộ số lượng dữ liệu có thể có của đối tượng cần xử lý thống kê. Ví dụ, nếu đối tượng cần xử lý thống kê là “độ ẩm của trầm tích Đệ Tứ ở Việt Nam” thì quần thể là toàn bộ giá trị độ ẩm của đất trầm tích Đệ Tứ ở Việt Nam (độ ẩm của tất cả mẫu đất ở mọi vùng miền từ Nam ra Bắc, ở mọi độ sâu mà trầm tích Đệ Tứ xuất hiện ở Việt Nam).
- Tập mẫu: là một nhóm dữ liệu được lấy ngẫu nhiên từ quần thể. Tập mẫu có cỡ mẫu nhỏ hơn rất nhiều so với cỡ mẫu của quần thể.
- Nhóm “trạng thái giới hạn”:
+ Trạng thái giới hạn I: thiết kế nền theo sức chịu tải (khả năng chịu lực)
+ Trạng thái giới hạn II: thiết kế nền theo độ biến dạng - Nhóm “loại công trình”:
+ Công trình xây dựng
+ Công trình cầu và cống - Mức ý nghĩa (confidence level): ký hiệu là α. Giá trị thường dùng là 0.025, 0.05, 0.10
- Hệ số tin cậy (confidence coefficient): ký hiệu là (1–α). Giá trị thường dùng là 0.90, 0.95, 0.98
| Công trình xây dựng | Công trình cầu & cống | ||
| Trạng thái giới hạn I | 0.95 | 0.98 | |
| Trạng thái giới hạn II | 0.85 | 0.90 |
- Sum of squared deviations of the X’s from their mean: \[S_{xx}=\sum \left ( x_i-\bar{x} \right )^{2}=\sum \left(x_i^{2} \right)-\frac{1}{n}\left (\sum x_i \right )^{2} =\sum \left(x_i^{2} \right)-n\bar{x}^{2})\]
- Sum of squared deviations of the Y’s from their mean: \[S_{yy}=\sum \left (y_i-\bar{y} \right )^{2}=\sum \left(y_i^{2} \right)-\frac{1}{n}\left (\sum y_i \right )^{2} =\sum \left(y_i^{2} \right)-n\bar{y}^{2})\]
- Sum of XY cross products: \[S_{xy}=\sum \left ( x_i-\bar{x} \right )\left ( y_i-\bar{y} \right )=\sum x_iy_i -\frac{1}{n}\sum x_i \sum y_i =\sum x_iy_i-n\bar{x}\bar{y}\]
- Tổng bình phương độ lệch (Sum of squared errors): \[SSE=\sum \left ( \hat{y}_i-y_i \right )^{2}\]
- Sai số chuẩn của đường hồi quy (Standard error of the estimate hoặc Standard error of the regression): \[s_e=\sqrt{\frac{SSE}{n-2}}=\sqrt{\frac{\sum \left ( \hat{y}_i-y_i \right )^{2}}{n-2}}\]
2. Các tiêu chuẩn thường dùng:
Các tiêu chuẩn về công tác xử lý thống kê số liệu địa chất của Việt Nam được dịch (có bổ sung) từ các tiêu chuẩn xử lý thống kê số liệu địa chất của Nga.
| Tiêu chuẩn của Việt Nam | Tiêu chuẩn của Nga |
| Tiêu chuẩn ngành 20TCN74-1987 (Trong tiêu chuẩn này có rất nhiều lỗi chính tả, lỗi các ký hiệu các tham số…) |
ГОСТ 20522-1975 ГРУНТЫ – Метод статистической обработки результатов определений характеристик |
| TCXD 74:1987 (là tiêu chuẩn ngành 20TCN74–1987 được in lại vào năm 2002, có sửa vài lỗi và bổ sung thêm nhiều lỗi khác !!!) |
ГОСТ 20522-1996 ГРУНТЫ – Методы статистической обработки результатов испытаний |
| TCVN 9153:2012 (bổ sung phần xử lý thống kê cho thí nghiệm nén ba trục) |
ГОСТ 20522-2012 ГРУНТЫ – Методы статистической обработки результатов испытаний |
3. Tóm tắt trình tự xử lý thống kê số liệu địa chất theo TCVN 9153:
Sau khi đã phân chia các đơn nguyên địa chất công trình, số liệu địa chất của từng đơn nguyên địa chất được tập hợp và tiến hành xử lý thống kê theo trình tự sau:
Bước 1: Kiểm tra sai số thô theo chỉ số thống kê (gọi tắt là kiểm tra chỉ số thống kê)
Bước 2: Kiểm tra tính đúng đắn của việc phân chia đơn nguyên địa chất công trình (gọi tắt là kiểm tra hệ số biến động)
Bước 3: Tính trị tiêu chuẩn \(A^{tc}\)
Bước 4: Tính trị tính toán \(A^{tt}\) theo nhóm trạng thái giới hạn (tính nền theo sức chịu tải hay theo biến dạng) và theo dạng công trình (công trình xây dựng hay công trình cầu và cống) (xem Bảng 1)
Một số lưu ý:
- Các thông số địa chất thường được chia thành hai nhóm:
+ nhóm thông số vật lý (thành phần hạt, độ ẩm, khối lượng thể tích, giới hạn Atterberg, tỷ trọng hạt…) và
+ nhóm thông số cơ học (sức kháng cắt – thể hiện qua cặp thông số: góc ma sát trong và lực dính; tính nén lún – thể hiện qua hệ số nén lún, môđun biến dạng tương ứng với các cấp tải nén…) - Mỗi nhóm thông số (vật lý hoặc cơ học) có cách tính trị tiêu chuẩn và trị tính toán khác nhau.
- Một số công thức tính toán trong các tiêu chuẩn xử lý thống kê nêu trên là những công thức cổ điển, chỉ phù hợp khi tính toán thủ công hoặc dùng để tìm hiểu cơ sở lý thuyết, không phù hợp khi sử dụng các phần mềm xử lý thống kê chuyên dụng hiện nay.
- Ngoài ra, có một số công thức trong các tiêu chuẩn xử lý thống kê nêu trên đã được rút gọn cho phù hợp với mục đích xử lý số liệu địa chất, nên gây khó khăn cho người đọc khi cần tra cứu về công thức gốc thường được dùng trong chuyên ngành thống kê.
3. Diễn giải các bước tính toán khi xử lý thống kê số liệu địa chất theo TCVN 9153:
Để thuận tiện cho việc so sánh các công thức tính giữa hai lĩnh vực: a) tiêu chuẩn về xử lý thống kê số liệu địa chất và b) chuyên ngành toán thống kê, lĩnh vực “tiêu chuẩn về xử lý thống kê số liệu địa chất” được gọi tắt là “tiêu chuẩn địa chất”; lĩnh vực “chuyên ngành thống kê” được gọi tắt là “thống kê”.
Bước 1: KIỂM TRA CHỈ SỐ THỐNG KÊ
Trong tiêu chuẩn thống kê, chỉ số thống kê và hệ số biến động đều dùng ký hiệu V. Để tránh nhầm lẫn giữa hai khái niệm này, chỉ số thống kê sẽ được gọi là \(V_{stat}\); hệ số biến động được gọi là V.
| Tiêu chuẩn địa chất | Thống kê |
| Giá trị \(A_i\)(giá trị cực tiểu và cực đại) trong tập dữ liệu phải thỏa điều kiện: \(\left | A_i-\bar{A} \right |<V_{stat}\: \sigma_{tb}\)
trong đó: |
Phép kiểm Grubbs (một phía): \[G=\frac{\left | \bar{x}-x_{outlying} \right |}{S}\] với \(G\) tính theo công thức: trong đó, \(t_{\alpha/n,n-2}\) là trị tới hạn của phân phối Student có bậc tự do \(\left ( n-2 \right )\), mức ý nghĩa \(\alpha\) |
Nhận xét:
a) Phương pháp loại sai số thô này về thực chất là phép kiểm Grubbs (Grubbs’ test) được Frank E. Grubbs đề xuất lần đầu tiên vào năm 1950.
b) Thay vì phải tra bảng, chỉ số thống kê có thể được tính trực tiếp theo công thức do Grubbs đề nghị.
Bước 2: KIỂM TRA HỆ SỐ BIẾN ĐỘNG
| Tiêu chuẩn địa chất | Thống kê |
| Hệ số biến động \(V=\frac{s}{\bar{A}}\)
với là \(s\) là độ lệch chuẩn và \(\bar{A}\) là trị trung bình số học của thông số \(A\). Ngưỡng cho phép của hệ số biến động V đối với: Nếu thông số \(A\) có hệ số biến động vượt quá ngưỡng cho phép nêu trên thì cần phải lặp lại việc loại bỏ giá trị cực trị (giá trị cực đại hoặc cực tiểu) cho đến khi nào hệ số biến động nằm trong khoảng cho phép. |
Cách tính hệ số biến động \(V\) tương tự như ở "Tiêu chuẩn địa chất"
Để kiểm tra khả năng hợp nhất hai đơn nguyên, cần dùng phép kiểm F |
Nhận xét:
a) Việc kiểm tra hệ số biến động V để xác định các giá trị dị thường có thể có trong tập mẫu. Giá trị dị thường chưa hẳn là sai số thô mà có thể là do phân lớp không hợp lý. Giá trị dị thường có thể được chuyển sang đơn nguyên kề bên.
b) Một số ý kiến đề nghị dùng bảng tra hệ số biến động ở phụ lục 3 để làm tiêu chí đánh giá sai số thô ở bước 2. Điều này không hợp lý vì các hệ số biến động ở phụ lục 3 chỉ được dùng để tính toán số lượng mẫu tối thiểu cần thí nghiệm để đạt được độ lệch chuẩn mong muốn.
Bước 3: TÍNH TRỊ TIÊU CHUẨN
| Tiêu chuẩn địa chất | Thống kê |
| A. Thông số vật lý: | |
| Với thông số vật lý, trị tiêu chuẩn là trị trung bình số học (sau khi đã loại sai số thô ở bước 1 và bước 2) | Cách tính trị trung bình số học tương tự cách tính ở "Tiêu chuẩn địa chất" |
| B. Sức kháng cắt | |
|
Sức kháng cắt thể hiện qua cặp giá trị: góc ma sát trong (\(\phi\)) và lực dính \(C\). Vì góc ma sát trong và lực dính không phải là chỉ tiêu thí nghiệm trực tiếp mà chỉ là chỉ tiêu tính toán từ tập hợp các giá trị ứng suất pháp (\(P_i\)) và ứng suất cắt (\(\tau_i\)) bằng phương pháp bình phương cực tiểu (least squares method) nên việc xử lý thống kê phải được thực hiện trên các giá trị ứng suất cắt \(\tau_i\) chứ không thực hiện trên cặp thông số góc ma sát trong và lực dính. Việc kiểm tra và loại sai số thô cho ứng suất cắt \(\tau_i\) phải được thực hiện riêng cho từng cấp áp lực nén \(P_i\). Sau khi đã loại hết sai số thô theo bước 1 và bước 2 cho ứng suất cắt \(\tau_i\) ở các cấp tải nén \(P_i\), trị tiêu chuẩn của góc ma sát trong và lực dính được tính theo công thức sau: \[tan\phi^{tc}=\frac{1}{\Delta}\left ( n\sum \tau_i P_i -\sum \tau_i\sum P_i\right )\] \[C^{tc}=\frac{1}{\Delta}\left ( \sum \tau_i \sum P_i^{2} -\sum P_i\sum \tau_iP_i\right )\] \[C^{tc}=\frac{1}{n}\left ( \sum \tau_i-tan\phi^{tc}\sum P_i \right )\] với: \(\Delta=n\sum P_i^{2}-\left (\sum P_i \right )^{2}\) Nếu \(C^{tc}<0\) thì lấy \(C^{tc}=0\) |
Phương trình hồi quy tuyến tính của \(y\) theo \(x\): \(y=b_o+b_1x\) \[b_1=\frac{S_{xy}}{S_{xx}}=\frac{\sum \left ( x_i-\bar{x} \right )\left ( y_i-\bar{y} \right )}{\sum \left ( x_i-\bar{x} \right)^2}\] \[b_1=\frac{\sum x_iy_i-\frac{\sum x_i\sum y_i}{n}}{\sum x_i^2-\frac {\left ( \sum x_i \right )^2}{n}}\] \[b_1=\frac{\sum x_iy_i-n\bar{x}\bar{y}}{\sum x_i^2-n\bar{x}^2}\] \[b_o=\bar{y}-b_1\bar{x}=\frac{1}{n}\left ( \sum y_i -b_1\sum x_i\right )\] Nếu so sánh với tiêu chuẩn địa chất: \[\Delta=nS_{xx}\] \(x_i, y_i\) tương ứng với \(P_i, \tau_i\) và \(b_o, b_1\) tương ứng với \(C^{tc}, tan\phi^{tc}\) Có thể trích giá trị \(b_o, b_1\) từ hàm LINEST của Excel hoặc các phần mềm xử lý thống kê chuyên dụng khác mà không cần dùng công thức phức tạp như TCVN 9153 đề nghị. |
| C. Tính nén lún | |
|
Hệ số nén lún \(a\) và môđun biến dạng \(E\) là các chỉ tiêu tính toán, được tính từ quan hệ giữa các cấp tải nén \(P_i\) và các hệ số rỗng \(e_i\) tương ứng. Vì vậy, tương tự như sức kháng cắt, việc kiểm tra và loại sai số thô cho các thông số tính nén lún phải được thực hiện cho các giá trị hệ số rỗng \(e_i\) của từng cấp tải nén \(P_i\). Sau khi đã loại hết sai số thô theo bước 1 và bước 2, trị tiêu chuẩn của hệ số nén lún \(a\) và môđun biến dạng \(E\) của từng cấp tải nén được tính theo trị tiêu chuẩn của hệ số rỗng ứng với từng cấp tải nén: \(a^{tc}=\frac{e_{i-1}^{tc}-e_{i}^{tc}}{P_{i}-P_{i-1}}\) \(E_i^{tc}=\frac{1+e_o^{tc}}{a_i^{tc}}\beta \cdot m_k\) với \(\beta\) và \(m_k\) lấy từ bảng tra ở Phụ lục 5 |
|
Nhận xét:
Việc tính góc ma sát trong \(\phi^{tc}\) và lực dính \(C^{tc}\) theo cặp thông số ứng suất nén \(P_i\) và ứng suất cắt \(\tau_i\) bằng phương pháp bình phương cực tiểu là bài toán xác định các hệ số của phương trình hồi quy tuyến tính của \(y\) theo \(x\): \(y=\beta_o+\beta_1 x\), với \(\beta_o, \beta_1\) là các hệ số của phương trình hồi quy tuyến tính của quần thể.
Do dữ liệu thí nghiệm thu thập được chỉ là một tập dữ liệu nhỏ, đại diện cho toàn bộ quần thể nên phương trình hồi quy tuyến tính của quần thể được ước lượng bằng phương trình hồi quy tuyến tính của tập mẫu đại diện: \(y=b_o+b_1x\). Ở đây, \(b_o\) tương ứng với \(C^{tc}\) và \(b_1\) tương ứng với \(tan\phi^{tc}\).
Bước 4: TÍNH TRỊ TÍNH TOÁN
Việc tìm trị tính toán của một thông số là bài toán tìm khoảng tin cậy \(CI\) (confidence interval) của trị trung bình (trị tiêu chuẩn) của thông số đó khi dùng trị trung bình này (của tập mẫu) làm ước lượng cho trị trung bình của quần thể.
Khi dùng giá trị trung bình của tập mẫu để ước lượng cho giá trị trung bình của quần thể, luôn có sai số. Sai số đó được thể hiện qua thông số “sai số chuẩn”, ký hiệu là SE (standard error): \(SE=\frac{s}{\sqrt{n}}\), với \(s\) là độ lệch chuẩn của tập mẫu, \(n\) là cỡ mẫu.
Tùy vào loại thông số (thông số vật lý hay thông số cơ học), cách tính trị tính toán sẽ khác nhau.
Khoảng tin cậy một phía (one-tail confidence interval) của trị trung bình của tập mẫu là:
\[CI=\bar{x}\pm t_{\alpha,n-1}SE=\bar{x}\pm t_{\alpha,n-1}\frac{s}{\sqrt{n}}\]
Khoảng tin cậy một phía của các hệ số của đường hồi quy tuyến tính \(y=b_o+b_1x\):
Khoảng tin cậy của hệ số \(b_1\): \(CI_{b_1}=b_1\pm t_{\alpha,n-2}SE_{b_1}\), với \(SE_{b_1}\) là sai số chuẩn (standard error) của hệ số \(b_1\).
\[SE_{b_1}=s_e\sqrt{\frac{n}{n\sum \left ( x_i^2 \right )-\left ( \sum x_i \right )^2}}=\frac{s_e}{\sqrt{S_{xx}}}=\sqrt{\frac{S_{yy}/S_{xx}-b_1^2}{n-2}}\]
Khoảng tin cậy của hệ số \(b_o\): \(CI_{b_o }=b_o \pm t_{\alpha,n-2}SE_{b_o }\), với \(SE_{b_o}\) là sai số chuẩn (standard error) của hệ số \(b_o\).
\[SE_{b_o}=s_e\sqrt{\frac{\sum \left ( x_i^2 \right )}{n\sum \left ( x_i^2 \right )-\left ( \sum x_i \right )^2}}=s_e\sqrt{\frac{1}{n}+\frac{\bar{x}^2}{S_{xx}}} = \sqrt{\frac{s_e^2}{n}+\left ( SE_{b_1} \bar{x}\right )^2}\]
| Tiêu chuẩn địa chất | Thống kê | ||||||||||
| A. Thông số vật lý |
|||||||||||
|
Trong TCVN 9153, trị tính toán được tính từ trị tiêu chuẩn theo công thức sau: \[A^{tt}=A^{tc}\left ( 1\pm\rho \right )\] Với thông số vật lý, chỉ số độ chính xác \(\rho= t_{\alpha,n-1} \frac{V}{\sqrt{n}} \), với \(V\) là hệ số biến động, \(n\) là cỡ mẫu. \[A^{tt}=A^{tc}\left ( 1\pm \rho \right )\]
|
Thông số \(A^{tc}, A^{tt}\) trong "Tiêu chuẩn địa chất" tương ứng với thông số \(\bar {x}, \mu \) trong "Thống kê". Khoảng tin cậy một phía của thông số vật lý: \[\mu=\bar{x} \pm t_{\alpha,n-1}SE =\bar{x} \pm t_{\alpha,n-1}\frac{s}{\sqrt{n}} =\bar{x} \pm t_{\alpha,n-1}\frac{V\bar{x}}{\sqrt{n}} =\bar{x}\left ( 1\pm t_{\alpha,n-1} \frac{V}{\sqrt{n}} \right )\] Nếu đặt \(rho=t_{\alpha,n-1} \frac{V}{\sqrt{n}}\) thì công thức tính trị tính toán theo trị tiêu chuẩn có thể được viết lại: \[\mu =\bar {x} \left ( 1\pm\rho \right )\] Công thức này tương đương với công thức tính trị tính toán cho thông số vật lý của "Tiêu chuẩn thống kê" |
||||||||||
| B. Sức kháng cắt | |||||||||||
| Với thông số sức kháng cắt, chỉ số độ chính xác của các hệ số \(b_o, b_1\):
\[\rho_{b_o}=t_{\alpha,n-2}V_{b_o}\] \[\rho_{b_1}=t_{\alpha,n-2}V_{b_1}\] |
Sai số chuẩn của các hệ số \(b_o, b_1\): \[SE_{b_o}=s_e\sqrt{\frac{\sum \left ( x_i^2 \right )}{n\sum \left ( x_i^2 \right )-\left ( \sum x_i \right )^2}}\] \[SE_{b_1 }=s_e\sqrt{\frac{n }{n\sum \left ( x_i^2 \right )-\left ( \sum x_i \right )^2}}\] \[V_{b_o}=\frac{s_{b_o}}{b_o}\approx\frac{SE_{b_o}}{b_o}\] \[V_{b_1}=\frac{s_{b_1 }}{b_1 }\approx\frac{SE_{b_1 }}{b_1 }\] Khoảng tin cậy một phía của hệ số \(b_o\): \[b_o\pm t_{\alpha,n-2}SE_{b_o}=b_o\pm t_{\alpha,n-2}\: b_oV_{b_o}=b_o\left ( 1\pm t_{\alpha,n-2}V_{b_o}\right )=b_o\left ( 1\pm \rho_{b_o} \right )\]với \(\rho_{b_o}=t_{\alpha,n-2}V_{b_o}\) Khoảng tin cậy một phía của hệ số \(b_1\): \[b_1 \pm t_{\alpha,n-2}SE_{b_1 }=b_o\pm t_{\alpha,n-2}\: b_1V_{b_1 }=b_1 \left ( 1\pm t_{\alpha,n-2}V_{b_1 }\right )=b_1 \left ( 1\pm \rho_{b_1} \right )\] với \(\rho_{b_1}=t_{\alpha,n-2}V_{b_1}\) |
||||||||||
|
Khoảng tin cậy cho lực dính \(C^{tc}\): \[C^{tt}=C^{tc}\left ( 1\pm \rho_C \right )\] với: \[\rho_C=t_{\alpha,n-2}V_C\]
\[C^{tt}=C^{tc}\left ( 1\pm \rho_C \right )\] \[C^{tt}=C^{tc}\left ( 1\pm t_{\alpha,n-2}\frac{\sigma_C}{C^{tc}} \right ) \] \[C^{tt}=C^{tc}\pm t_{\alpha,n-2}\: \sigma_t\sqrt{\frac{1}{\Delta}\sum P_i^2}\] |
Khoảng tin cậy một phía của \(b_o\): \[CI_{b_o}=b_o+t_{\alpha,n-2}SE_{b_o}\] \[SE_{b_o}=s_e\sqrt{\frac{\sum x_i^2}{n\sum x_i^2-\left ( \sum x_i \right )^2}}\] Như vậy, nếu \(b_o\) tương ứng với \(C^{tc}, \sigma_t=s_e, \Delta=nS_{xx}=n\sum x_i^2-\left ( \sum x_i \right )^2\) thì: \[b_o\pm t_{\alpha,n-2}\: SE_{b_o}=C^{tc}\pm t_{\alpha,n-2}\: \sigma_t\sqrt{\frac{1}{\Delta}\sum P_i^2}\] Công thức này tương đương với công thức tính trị tính toán cho lực dính của "Tiêu chuẩn thống kê" Giá trị \(SE_{b_o}\) có thể trích từ hàm LINEST của Excel hoặc các phần mềm xử lý thống kê chuyên dụng khác mà không cần dùng công thức phức tạp như TCVN 9153 đề nghị. |
||||||||||
|
Khoảng tin cậy một phía cho góc ma sát trong \(tan\phi^{tc}\): \[tan\phi^{tt}=tan\phi^{tc}\left ( 1\pm \rho_{tan\phi} \right )\] với: \[\rho_{tan\phi}=t_{\alpha,n-2}V_{tan\phi}\]
\[tan\phi^{tt}=tan\phi^{tc}\left ( 1\pm \rho_{tan\phi} \right )\] \[tan\phi^{tt}=tan\phi^{tc}\left ( 1\pm t_{\alpha,n-2}\frac{\sigma_{tan\phi}}{tan\phi^{tc}} \right ) \] \[tan\phi^{tt}=tan\phi^{tc}\pm t_{\alpha,n-2}\: \sigma_t\sqrt{\frac{n}{\Delta}}\] |
Khoảng tin cậy một phía của \(b_1\): \[CI_{b_1}=b_1+t_{\alpha,n-2}SE_{b_1}\] \[SE_{b_1}=s_e\sqrt{\frac{n}{n\sum x_i^2-\left ( \sum x_i \right )^2}}=\frac{s_e}{\sqrt{S_{xx}}}\] Như vậy, nếu \(b_1\) tương ứng với \(tan\phi^{tc}, \sigma_t=s_e, \Delta=nS_{xx}=n\sum x_i^2-\left ( \sum x_i \right )^2\) thì: \[b_1\pm t_{\alpha,n-2}\: SE_{b_1}=tan\phi^{tc}\pm t_{\alpha,n-2}\: \frac{\sigma_t}{\sqrt{S_{xx}}}=tan\phi^{tc}\pm t_{\alpha,n-2}\: \sigma_t\sqrt{\frac{n}{\Delta}}\] Công thức này tương đương với công thức tính trị tính toán cho góc ma sát trong của "Tiêu chuẩn thống kê" Có thể trích giá trị \(SE_{b_1}\) từ hàm LINEST của Excel hoặc các phần mềm xử lý thống kê chuyên dụng khác mà không cần dùng công thức phức tạp như TCVN 9153 đề nghị. |
||||||||||
| C. Tính nén lún | |||||||||||
| Cách tính trị tính toán cho hệ số nén lún \(a\) và môđun biến dạng \(E\) tương tự như cách tính trị tính toán cho thông số vật lý | |||||||||||
Nhận xét:
a) Khoảng tin cậy của các hệ số \(b_o, b_1\) có thể được tính trực tiếp từ trị số \(SE_{b_o}, SE_{b_1}\) (luôn được cung cấp cùng với các hệ số phương trình hồi quy tuyến tính khi dùng các phần mềm thống kê), mà không cần phải tìm các chỉ số độ chính xác \(\rho_{b_o}, \rho_{b_1}\) từ các công thức tìm độ lệch chuẩn \(\sigma_{tan\phi}, \sigma_C\) rất phức tạp như trong TCVN 9153 đề nghị.
b) Ngoài ra, các hệ số biến động \(V_{b_o}, V_{b_1}\) tính theo TCVN 9153 thực chất không phải là hệ số biến động của góc ma sát trong \(\phi^{tc}, C^{tc}\) của tập mẫu nên không thể dùng tiêu chí đánh giá sai số thô ở bước 2 để đánh giá các hệ số biến động này.
5. Ứng dụng Microsoft Excel để tính trị tính toán cho sức kháng cắt:
a) Trích giá trị \(b_o, b_1, SE_{b_o}, SE_{b_1}\) từ hàm LINEST của Excel:
Hàm LINEST của Excel sẽ trả về một mảng gồm 5 hàng và 2 cột. Để tính khoảng tin cậy của \(b_o, b_1\), chỉ cần dùng 4 giá trị đầu tiên của hàm LINEST.
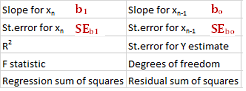
b) Tính trị tới hạn \(t_{\alpha,n-2}\):
Để tính trị tới hạn \(t_{\alpha,n-2}\), Microsoft Excel có các hàm TINV (với Excel 2003), T.INV và T.INV.2T (với Excel 2010 trở về sau).
Tuy nhiên, không hiểu vì sao Excel lại định nghĩa cách truyền tham số cho các hàm này rất rối rắm, không nhất quán, dễ gây nhầm lẫn cho người sử dụng (!).
Ví dụ, để tìm giá trị \(t_\alpha\) với hệ số tin cậy 95% \((\alpha=0.05)\), bậc tự do \((n-2=10)\) thì cách sử dụng các hàm này như sau:
| Hàm TINV | =TINV(2*(1-0.95),10) | =1.81 |
| Hàm T.INV | =T.INV(0.95,10) | =1.81 |
| Hàm T.INV.2T | =T.INV.2T(2*(1-0.95),10) | =1.81 |
6. Tài liệu tham khảo:
- Bộ Khoa học và Công nghệ (2012). TCVN 9153:2012: Công trình thủy lợi — Phương pháp chỉnh lý kết quả thí nghiệm mẫu đất.
- Bộ Xây dựng (1990). Tiêu chuẩn ngành 20TCN74-87: Đất xây dựng — Phương pháp chỉnh lý thống kê các kết quả xác định các đặc trưng của chúng. Nhà xuất bản Bộ Xây dựng
- Bộ Xây dựng (2002). TCXD 74 – 1987: Đất xây dựng — Phương pháp chỉnh lý thống kê các kết quả xác định các đặc trưng của chúng. Nhà xuất bản Xây dựng
- Frank E. Grubbs (1950). Sample Criteria for Testing Outlying Observations. The Annals of Mathematical Statistics, Vol. 21, No. 1, pp. 27-58. Institute of Mathematical Statistics
- John E. Freund (1967). Modern Elementary Statistics, 3rd edition. Prentice-Hall, Inc. New Jersey
- Neil A. Weiss (2012). Introductory Statistics, 9th edition. Pearson Education, Inc.
[Online]:












