When working with technical documents, readers are often deal with specific terms “accuracy” and “precision”. The question is if these terms have the same meanings?
When working with technical documents, readers are often deal with specific terms First of all, it is confirmed that the terms “accuracy” and “precision” are completely different. However because these terms are sometimes translated into Vietnamese using the same Vietnamese word so it makes readers confused.
The term “accuracy” is used to describe the difference between measured values with the "true" value or "referenced" value. Therefore, the term "accuracy" relates to the bias or system error of the measurement system.
The term “precision” is used to describe the closeness or the repeatability of measured values under the same measurement environment. Therefore, the term "precision" relates to the variation of measured values.
The dart board is often used to illustrate the difference between "accuracy" and "precision" (see figure below):
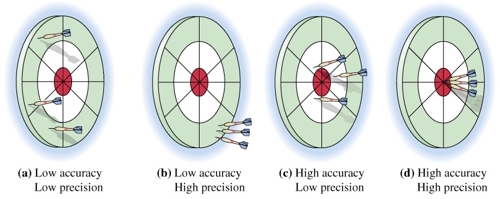
(Source: http://cwx.prenhall.com/bookbind/pubbooks/hillchem3/medialib/media_portfolio/01.html)
Figure a: Because three arrows are neither close to each other nor close to the bull's eye so this test is considered as low accuracy and low precision.
Figure b: Because three arrows are close to each other but not close to the bull's eye so this test is considered as low accuracy (too far from the "true" value -- bull's eye) and high precision (good repeatability).
Figure c: Because three arrows are not close to each other but close to the bull's eye so this test is considered as high accuracy (not far from the "true" value -- bull's eye) and low precision (bad repeatability).
Figure d: Because three arrows are not only close to each other but also close to the bull's eye so this test is considered as high accuracy and high precision.